行程问题研究的是物体在运动的过程中,路程、速度以及时间三者之间的关系。行程问题根据题型可以分为相遇问题和追及问题,其中相遇可以分为直线上的相遇和环形的相遇,追及也可以分为直线上的追及和环线上的追及。
行程问题的解决可以利用六大数学思想中的数形统一思想、综合化归思想。例如:我们可以利用数形结合思想从题干条件中提取出图形条件,再根据图形条件找出等量关系,从而求出未知量;还可以采用综合化归思想,利用特值法、比例法来解决问题。下面我们通过几个例子来具体介绍如何解决行程问题。
1、利用数形统一思想来解决行程问题。
例一、甲乙两同学从跑道的一端前往另一端,甲在全部时间的一半内跑,另一半时间内走,乙在全部路程的一半内跑,另一半路程内走。如果他们跑和走的速度分别相等,则先到终点的是:()
A、甲 B、乙 C、同时到终点 D、无法判断
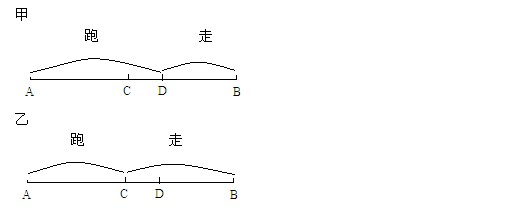
【中公解析】题目中要求的事先到达终点的,也就是求从A点到B点甲乙中用时间比较少的。利用数形统一思想解题,设整个路程AB的中点为C点,D点为甲一半时间内跑所到达的点。跑的速度大于走的速度,相同的时间内跑的路程大于走的路程,所以D点应在中点C点的右边,如图所示位置。根据图形条件,我们发现,AC段甲乙都是跑的,跑的速度相等,路程相同,所以时间相等;同理DB段的甲乙都是走的,走的速度相同,路程相同,所以时间相等。CD段,甲用跑的,乙用走的,跑的速度大于走的速度,所以甲用的时间比乙少,所以甲先到终点,选A.
2、利用特值法解题
例二、A、B两地间有条公路,甲乙二人分别从A、B两地出发相向而行,甲先走半小时,乙才出发,一小时后两人相遇,甲的速度是乙的2/3。问甲乙所走的路程之比是()
A.5:6 B.1:1 C.6:5 D.4:3
【中公解析】由题意,设甲的速度为2,乙的速度为3,则甲先走半小时,一小时后相遇,总共走的时间是1.5小时,甲走的路程是2×1.5=3,乙走的路程为3×1=3.故甲乙所走的路程之比为1:1.选B。
3、利用比例法解题
例三、小王步行的速度比跑步慢50%,跑步的速度比骑车慢50%。如果他骑车从A城去B成,再步行返回A城共需要2小时。问小王跑步从A城到B城需要多少分钟?
A、45 B、48 C、56 D、60
【中公解析】由题意,跑步的速度与步行的速度之比为2:1,骑车的速度与跑步的速度之比为2:1,根据连比的性质,骑车的速度与步行的速度之比为4:1。路程相等时,时间之比等速度之比的反比。所以小王骑车从A城去B成,再步行返回A城所花的时间之比为1:4,又总时间为2小时,所以步行所花的时间为2÷5×4=1.6小时。所以小王跑步从A城到B城需要的时间为1.6÷2=0.8小时。
总结:行程问题的解题技巧性比较强,需要考生在平时加强联系,能够熟练运用各种方法解题。
设为首页 | 加入收藏 | 关于我们 | 联系方式 | 版权声明 | 招生代理 | 支付方式 | 网站地图 | 手机页面 | 友情链接
Copyright©1999-2017 北京中公未来教育咨询有限公司 .All Rights Reserved京ICP备10218183号 京ICP证161188号  京公网安备11010802020593号 出版物经营许可证新出发京批字第直130052号
京公网安备11010802020593号 出版物经营许可证新出发京批字第直130052号